
Jeppe Revall Frisvad
Associate Professor in Computer Graphics, M.Sc.(Eng.), Ph.D.Visual Computing
DTU Compute
Technical University of Denmark
Contact information
Home
Publications
Teaching
Code Packages
Press Appearances
 |
Jeppe Revall FrisvadAssociate Professor in Computer Graphics, M.Sc.(Eng.), Ph.D.Visual Computing DTU Compute Technical University of Denmark Contact information Home Publications Teaching Code Packages Press Appearances |
xDDiff: Multidimensional optical diffusion for the measurement of appearance [2024-2027]
External beneficiary. EURAMET EMPIR joint research project (JRP) co-funded by Horizon Europe and participating states.
CORALS: New strategies for harvesting solar energy using coral-inspired microgeometry [2024-2026]
Principal investigator together with Michael Kühl. Project funded by Villum Synergy.
Modelling Optical Properties of Teeth and Gingiva [2022-2024]
University partner. Project funded by Innovation Fund Denmark.
A World of Digital Grains of Sand [2022]
Co-applicant. Project funded by Danish Board of Business Development through Vision Denmark.
ExCheQuER: Examining Cheese Quality Elements and Reactions [2021-2025]
Leader of WP3: Optical Sensors. Project funded by Innovation Fund Denmark.
PRIME: Predictive Rendering In Manufacture and Engineering [2020-2025]
Beneficiary. Innovative Training Network (ITN) funded by EU Horizon 2020.
BxDiff: New Quantities for the Measurement of Appearance [2019-2022]
External funded partner. EURAMET EMPIR joint research project (JRP) co-funded by EU Horizon 2020 and participating states.
ApPEARS: Appearance Printing - European Advanced Research School [2019-2023]
Beneficiary. Innovative Training Network (ITN) funded by EU Horizon 2020.
Virtual Reality-Based Visualization of Geometric Data [2018-2022]
Participant. Project funded by Advokat Bent Thorbergs Fond.
MADE Digital: Driving Growth and Productivity in Manufacturing Through Digitalization [2017-2020]
Leader of WP9: Sensor Technology and Production Data. Project funded by Innovation Fund Denmark.
3DIMS: 3D-Printing Integrated Manufacturing System [2017-2019]
Leader of WP5: Industry 4.0. Project funded by Innovation Fund Denmark.
FlexDraper: An Intelligent Robot-Vision System for Draping Fiber Plies [2016-2019]
Participant. Project funded by Innovation Fund Denmark.
QRprod: QR Coding in High-Speed Production of Plastic Products and Medical Tablets [2016-2019]
Leader of WP4: Image Processing and Data Management. Project funded by Innovation Fund Denmark.
CIL2018: NextGen Scanner for Checked In Luggage [2016-2019]
Participant. Project funded by Innovation Fund Denmark.
MADE SPIR: Strategic Platform for Innovation and Research [2014-2019]
Leader of WP9: Sensors and Quality Control. Project funded by Innovation Fund Denmark.
Eco3D: The Cyber-Physical 3D Ecosystem [2014-2024]
Co-founder. Framework for exploiting synergies within our Section for Visual Computing.
Digital Prototypes [2011-2012]
Participant. Project funded by the Danish
Council for Technology and Innovation (Resultatkontrakt).
GPUlab: Desktop Scientific Computing [2010-2013]
Co-applicant. Project funded by the Danish Council for Independent Research - Technology and Production Sciences (FTP).
CIFQ: Center for Imaging Food Quality [2010-2015]
Participant. Project funded by the Danish Council for Strategic Research.
with journal papers highlighted by a background color.
 |
Quantitative measurement of the anisotropy of a turbid medium using polarization imaging Lezhong Wang, Pawel Tomasz Pieta, Siavash Arjomand Bigdeli, Niels Christian Krieger Lassen, Anders Nymark Christensen, Anders Bjorholm Dahl, Jeppe Revall Frisvad Applied Optics. 2025. To appear. |
 |
Characterization and quantification of anisotropy in mozzarella cheese: exploring the impact of structural anisotropy on functional properties using complementary analytical technologies Harshkumar Patel, Pawel Tomasz Pieta, Lezhong Wang, Siavash Bigdeli, Anders Nymark Christensen, Anders Bjorholm Dahl, Jeppe Revall Frisvad, Kristina Schmidt Bejder, Joana Ortega, Ulf Andersen, Søren Balling Engelsen, Frans W. J. van den Berg Food Structure 44, Article 100425. April 2025. |
 |
Feature-centered first order structure tensor scale-space in 2D and 3D Pawel Tomasz Pieta, Anders Bjorholm Dahl, Jeppe Revall Frisvad, Siavash Arjomand Bigdeli, Anders Nymark Christensen IEEE Access 13, pp. 9766-9779. January 2025. |
 |
NeuPreSS: compact neural precomputed subsurface scattering for distant lighting of heterogeneous translucent objects Thomson TG, Jeppe Revall Frisvad, Ravi Ramamoorthi, Henrik Wann Jensen Computer Graphics Forum (PG 2024) 43(7), Article e15234. October 2024. [lowres pdf] [video] |
| Digitizing the appearance of 3D printing materials using a spectrophotometer Alina Pranovich, Morten Rieger Hannemose, Janus Nørtoft Jensen, Duc Minh Tran, Henrik Aanæs, Sasan Gooran, Daniel Nyström, Jeppe Revall Frisvad Sensors 24(21), Article 7025. October 2024. [abstract] |
|
 |
Empirical BRDF model for goniochromatic materials and soft proofing with reflective inks Alina Pranovich, Jeppe Revall Frisvad, Sergiy Valyukh, Sasan Gooran, Daniel Nyström IEEE Computer Graphics & Applications 44(5), pp. 143-152. September/October 2024. [abstract/demo] |
 |
Practical error estimation for denoised Monte Carlo image synthesis  Arthur Firmino, Ravi Ramamoorthi, Jeppe Revall Frisvad, Henrik Wann Jensen SIGGRAPH 2024 Conference Proceedings, pp. 93:1-93:10. ACM, July 2024. [lowres pdf] |
 |
Neural SSS: lightweight object appearance representation Thomson TG, Duc Minh Tran, Henrik Wann Jensen, Ravi Ramamoorthi, Jeppe Revall Frisvad Computer Graphics Forum (EGSR 2024) 43(4), Article e15158. July 2024. [lowres pdf] |
 |
Practical appearance model for foundation cosmetics Dario Lanza, Juan Raúl Padrón Griffe, Alina Pranovich, Adolfo Muñoz, Jeppe Revall Frisvad, Adrián Jarabo Computer Graphics Forum (EGSR 2024) 43(4), Article e15148. July 2024. [lowres pdf] [webpage] |
 |
StereoDiffusion: training-free stereo image generation using latent diffusion models  Lezhong Wang, Jeppe Revall Frisvad, Mark Bo Jensen, Siavash Arjomand Bigdeli CVPR 2024 Workshop on Generative Models for Computer Vision, pp. 7416-7425. June 2024. [lowres pdf] [supplement] [code] [OpenAccess] |
 |
Digitizing translucent object appearance by validating computed optical properties Duc Minh Tran, Mark Bo Jensen, Pablo Santafé-Gabarda, Stefan Källberg, Alejandro Ferrero, Morten Rieger Hannemose, Jeppe Revall Frisvad Applied Optics 63(16), pp. 4317-4331. June 2024. [data] [simulator] |
 |
Bidirectional reflectance measurements over a micrometric surface area using a goniospectrophotometer Dipanjana Saha, Lou Gevaux, Jeppe Revall Frisvad, Gaël Obein Review of Scientific Instruments 95(5), Article 055114. May 2024. |
 |
Influence of the printing direction on the surface appearance in multi-material fused filament fabrication Riccardo Tonello, Md. Tusher Mollah, Kenneth Weiss, Jon Spangenberg, Are Strandlie, David Bue Pedersen, Jeppe Revall Frisvad Computer-Aided Design and Computer Graphics (CAD/Graphics 2023), pp. 90-107. Lecture Notes in Computer Science, Vol. 14250. Springer, February 2024. [lowres pdf] [poster] |
We presented a state-of-the-art report on models for acquiring the optical properties of materials at Eurographics 2020:
Survey of models for acquiring the optical properties of translucent materials 
Jeppe Revall Frisvad, Søren Alkærsig Jensen, Jonas Skovlund Madsen, António Correia, Li Yang, Søren Kimmer Schou Gregersen, Youri Meuret, Poul-Erik Hansen Computer Graphics Forum (EG 2020) 39(2), pp. 729-755. May 2020. [webpage] [OpenAccess] |
This publication includes a table providing an overview of the various types of models available up to 2020 and how they operate on different scales. A convenient online version of this table is available in the webpage accompanying the publication.
02941 Physically Based Rendering and Material Appearance Modelling (since spring 2016)
Course responsible and course designer. PhD course.
02562 Rendering - Introduction (since Autumn 2011)
Course responsible.
02561 Computer Graphics (since Autumn 2015)
Course responsible.
High-Performance Graphics 2025 (local chair)
Computer Graphics International 2023 (program committee member)
Pacific Graphics 2024 (program committee member)
Pacific Graphics 2022 (program committee member)
EGSR 2025 (conference chair)
EGSR 2022 (program committee member)
EGSR 2021 (program committee member)
EGSR 2020 (program committee member)
SIGGRAPH Asia 2025 (technical papers committee member)
SIGGRAPH Asia 2022 (technical papers committee member)
SIGGRAPH Asia 2020 (technical papers conflict of interest coordinator)
Eurographics 2020 (tutorials co-chair)
Eurographics 2015 (short papers international program committee member)
3DV 2018 Tutorial: Methods for photographic radiometry, modeling of light transport and material appearance (organizer and presenter)
ICCV 2017 Workshop: Data-Driven BxDF Models for Computer Vision Applications (chair and organizer)
Vision Day 2018 (session organizer)
Vision Day 2017 (conference chair)
Vision Day 2015 (session organizer)
Vision Day 2014 (conference chair)
Vision Day 2013 (session organizer)
Graphical Vision Day 2011 (program committee member)
Graphical Vision Day 2010 (co-chair)
Graphical Vision Day 2009 (co-chair)
ISVD 2011 (scientific committee member)
ISVD 2009 (program committee member)
Reviewer for SIGGRAPH, Eurographics, ACM Transactions on Graphics, Optica (AO, OE, JOSA A), Computer Graphics Forum.
Member of ACM SIGGRAPH and Eurographics Association.
May 2019
WebGL demonstrator of my procedural model for simulating pupillary hippus.
This model was published in a paper at Eurographics 2009, and it produces interesting dynamic effects for glare simulation.
The webpage includes a Matlab implementation of the model.
April 2018
Matlab code (inhLMabs) implementing a variation of the Lorenz-Mie theory for calculating the phase function of a spherical particle.
This variation includes the case where the particle scatters an inhomogeneous wave, which is the usual case in an absorbing medium.
The code accompanies an article in Journal of the Optical Society of America A.
March 2018
WebGL demonstrator for visualizing the phase function of spherical particles.
This demo visualizes the phase function given by the Lorenz-Mie theory and implemented using a paper from SIGGRAPH 2007.
I include a new technique for calculating the phase function of a spherical particle that scatters an inhomogeneous electromagnetic plane wave.
June 2017
Rendering Framework has been updated for the course 02941 Physically Based Rendering and Material Appearance Modelling.
March 2017
WebGL example updated to include recent improvements of my onb model by other authors.
October 2016
WebGL demonstrator for exploring noise functions. [Not working in Internet Explorer.]
This demo illustrates the qualities of sparse convolution noise as presented in my paper from GRAPHITE 2007,
but here implemented as a GLSL ES function.
January 2016
Rendering Framework has been updated for the course 02941 Physically Based Rendering.
December 2014
WebGL example of my onb method. It is here used to generate a consistently oriented tangent space.
November 2014
WebGL examples developed for the course 02560 Web Graphics and Scientific Visualization.
See the links in the section called Lecture Examples.
October 2014
WebGL example of our directional dipole for subsurface scattering is now available.
It accompanies the abstract of our paper to appear in ACM Transactions on Graphics.
June 2014
dirpole code has been released.
This is a simplistic example implementation of our directional dipole model for subsurface scattering.
It accompanies a publication to appear in ACM Transactions on Graphics.
June 2013
LMabs code has been published in a Matlab version.
This is code for computing the scattering properties of participating media using Lorenz-Mie theory.
It accompanies a publication that appeared in ACM Transactions on Graphics (SIGGRAPH 2007).
There has been much discussion and many misunderstandings about the work of the remarkable Danish scientist Ludvig Lorenz (1821-1891) on the theory of light scattering of a plane wave by a spherical particle. This theory is often referred to as Mie theory. In "The Scattering of Light and other electromagnetic radiation", Academic Press, 1969, Kerker presents a historical investigation of the origins of the theory and concludes:
It is not the intention of this author to arbitrate the questions of priority raised here nor to identify the theory of scattering by a sphere with any one man's name. Indeed, coincident and consecutive discoveries are common occurrences in science. But certainly if this theory is to be associated with the name or names of individuals, at least that of Lorenz, in whose paper are to be found the practical formulas so commonly used today, should not be omitted.
Nevertheless, some authors prefer to call it Mie theory rather than Lorenz-Mie theory. Perhaps because of the widespread supposition that Lorenz's theory relies on the existence of an ether. Reading the first pages of Lorenz's article, it is clear that this is certainly not true (see the translation below). Lorenz explicitly states that light propagation is like the laws for transmission of electricity and elastic forces, although it differs from the theory of elasticity in ruling out the possibility of longitudinal oscillations. Lorenz is thus working with transversal waves just like Maxwell and Mie. To uphold the recommendation that the theory of scattering of a plane wave by a spherical particle should continue to be called Lorenz-Mie theory, I decided to work on a translation of Lorenz's pioneering article from 1890.
My time available for working on this project has been very limited, and the project was on hold from 2011 to 2018. Helge Kragh then stepped in to revive the project and help complete it. This led to significant progress, so that there is now a complete first draft of the translation. The original article is:
Lorenz, L. Lysbevægelser i og uden for en af plane Lysbølger belyst Kugle. Det kongelige danske Videnskabernes Selskabs Skrifter, 6. Række, naturvidenskabelig og mathematisk Afdeling VI. 1-62. 1890. [lowres pdf]
The original article is 62 pages (one blank). The translation follows the original page numbering, and the pdf is available for download here:
Lorenz, L. Light propagation in and outside a sphere illuminated by plane waves of light. Det kongelige danske Videnskabernes Selskabs Skrifter 6(6), pp. 1-62. 1890. Translated by Jeppe Revall Frisvad and Helge Kragh, 2019.
In an old Danish Biographical Encyclopedia, the following interesting paragraph about this article appears. Translated from Danish:
Lorenz's work on the Theory of Colour Dispersion (Videnskab. Selsk. Skrifter 6. R. II, 1883) is particularly important as it is the outset of his solution of the old famous rainbow problem. The outlines of the rainbow theory are given by Descartes and Newton, more completely by Airy, who explained the supernumerary arcs by light interference. But, while one had previously limited oneself significantly to determining the directions in which these arcs appear, Lorenz set himself the goal to determine the light intensity completely in all directions on the basis of the theory of light. To complete this task, Lorenz worked almost continuously for several years; the dissertation is available in Videnskab. Selsk. Skrifter 6. R. VI (1890).
Our translation of Lorenz paper was published in European Physical Journal H together with an accompanying article describing the context and contents of Lorenz's work and surveying how it has been cited and used after its publication:
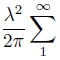 |
Light propagation in and outside a sphere illuminated by plane waves of light Ludvig Lorenz [translated by Jeppe Revall Frisvad and Helge Kragh] European Physical Journal H 44(2), pp. 77-135. August 2019. Translation of "Lysbevægelser i og uden for en af plane Lysbølger belyst Kugle". Det kongelige danske Videnskabernes Selskabs Skrifter 6(6):1-62, 1890. |
 |
On Ludvig Lorenz and his 1890 treatise on light scattering by spheres Jeppe Revall Frisvad and Helge Kragh European Physical Journal H 44(2), pp. 137-160. August 2019. [front cover image] |