02421 Stochastic Adaptive Control

Important note

This website is under construction and will be updated with more information. Please see the course database for more information.

Course description

In the course, we will develop control algorithms that can mitigate uncertainty and fluctuations from stochastic external disturbances. Specifically, the algorithms will combine methods for system identification (e.g., state and parameter estimation) and optimal control of stochastic systems into adaptive control algorithms that simultaneously identify and control the system. The course combines methods from courses on probability theory/statistics, control, time series analysis, and optimization, and it is relevant to many different study lines, including mathematical, electrical, chemical, and mechanical engineering.

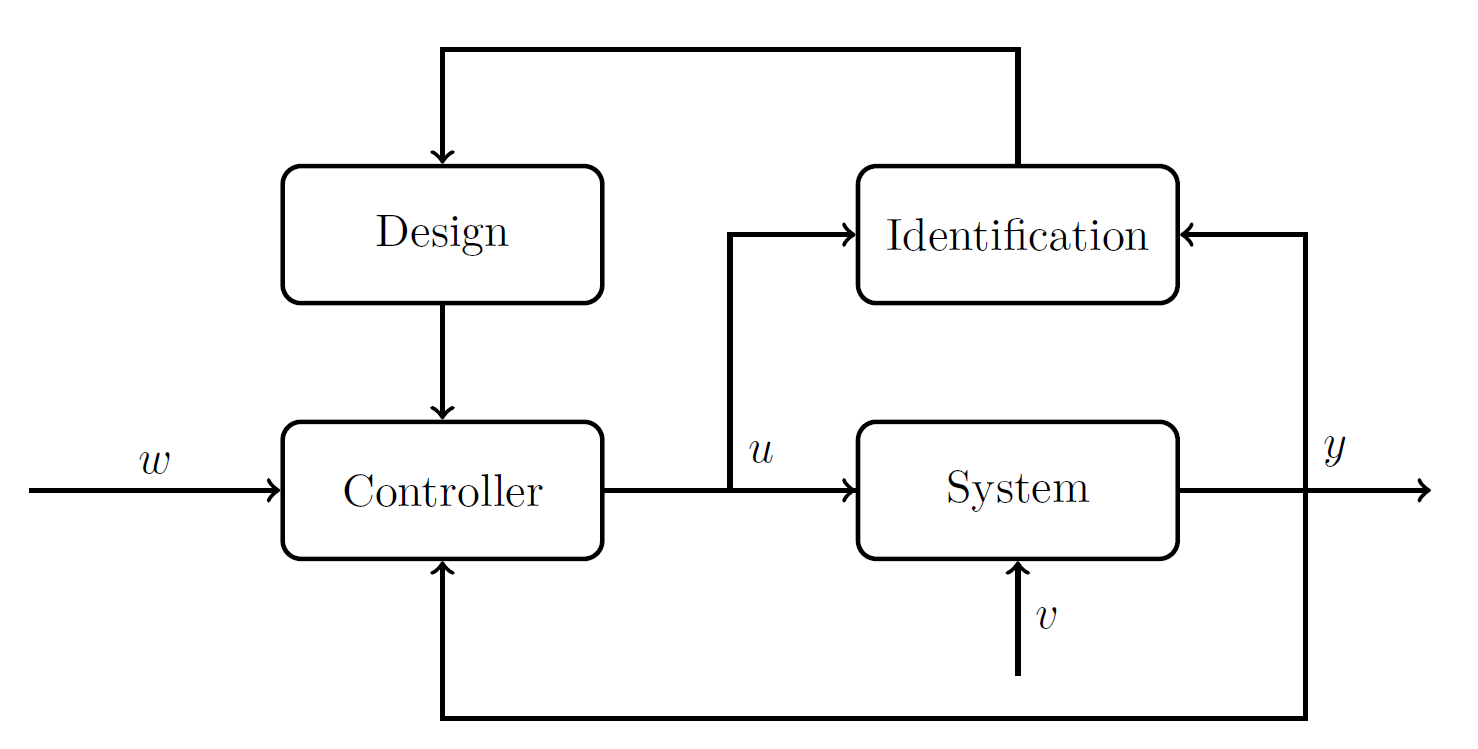The topic of the course is best illustrated with an example. The figure below shows the output (variables of interest), the manipulated inputs (the variables that we can determine), and the parameters (which we don't necessarily know) of a given process. At first, the system is not controlled, i.e., the manipulated inputs are independent of the system output (this is referred to as open-loop because there is no feedback). Consequently, the process output varies more than we would like it to and the process constraint (black dashed line) is occasionally violated. Next, we use a feedback control algorithm to stabilize the output (i.e., to squeeze the output). Now, the process is more well-behaved, but we have not gained anything economically. The next step is to shift the operating point closer to the process constraint. However, if there are changes in the process, or if we simply do not know it well enough, the feedback control might actually make things worse. In this example, we introduce a jump in one of the parameters towards the end of the simulation. The dashed lines indicate the true parameters and the solid lines are the values estimated by an adaptive controller. In the left and middle figure, we compare a feedback controller that is not adaptive (in blue) with a feedback controller that is adaptive (in red). Clearly, the adaptive controller is able to adjust in the final part of the simulation by increasing the manipulated input, and the control performance is not at all compromised. In this course, we will learn how to develop such adaptive controllers that can mitigate changes in the process and external disturbances.

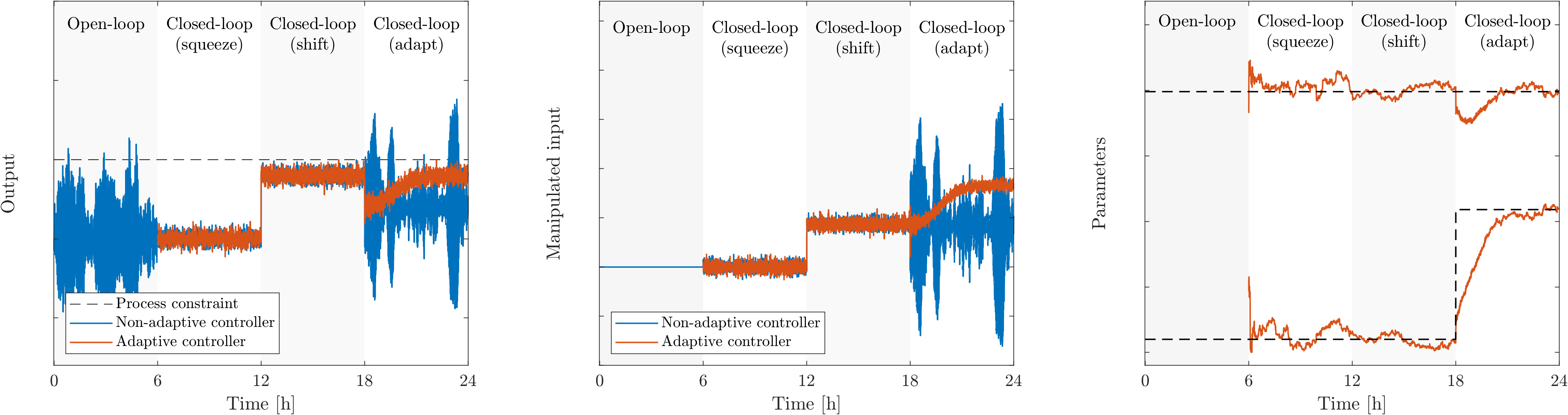Course information

The course is taught Tuesday 8-12 in the spring semester in Bldng. 421, Aud. 71. The exam consists of 4 mandatory assignments.

Course responsible

The course is taught by Tobias K. S. Ritschel.

Building 303B, office 052
Matematiktorvet
DK-2800 Kgs. Lyngby
Denmark

Phone: +45 4525 3315
Mobile: +45 6062 1486
E-mail: tobk@dtu.dk