


Discrete ill-posed problems arise, e.g., when one wants to compute information about interior properties using exterior measurements. The solutions to such problems are very sensitive to noise, and regularization methods must be used to stabilize the solutions, by imposing additional information about the solution.
The question then arises: which additional information to impose on the regularized solution?
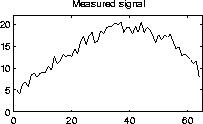
This dilemma is illustrated by an example from geomagnetic prospecting, in which we measure a noisy signal which consists of the vertical magnetic field at the surface of the earth, due to a magnetic iron ore deposit underneath the surface. The measured signal is shown in the left figure above.
Given a mathematical model of the connection between the magnetic field at the ore and at the surface (a Fredholm integral equation of the first kind), our goal is to compute the exact solution = the magnetic field at the iron ore. The following solutions are computed in Matlab, using the Regularization Tools software.
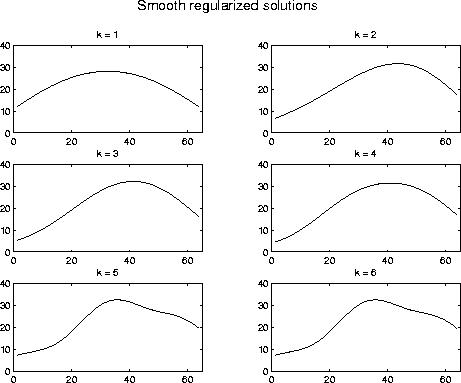
The above solutions are computed by requiring the regularized solutions to be continuous and smooth. The algorithm is called TSVD, and the parameter k controls the amount of smoothness: the smaller the k, the smoother the solution.
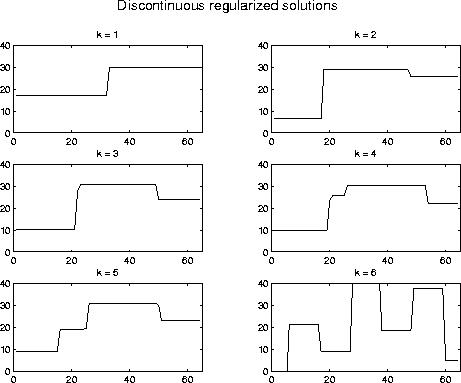
The above solutions are computed by requiring the regularized solution to be piecewise constant. This algorithm is called PP-TSVD, and the parameter k now controls the number of discontinuities.
Which regularized solution do you think is closest to the exact solution?
Make you guess before looking at the exact solution.