Copyright 2002 IEEE. To be published in the Proceedings of 2002 IEEE International Symposium on Circuits and Systems (ISCAS), Phoenix, Arizona, USA, May 26-29, 2002.

Residue Number System Reconfigurable Datapath

Gian Carlo Cardarilli, Andrea Del Re, Alberto Nannarelli and Marco Re
Department of Electrical Engineering
University of Rome "Tor Vergata" - Italy

http://dspvlsi.uniroma2.it/

Abstract

1  Introduction

Previous work demonstrated that FIR filters implemented in the Residue Number System (RNS) offer better performance of filters realized in the traditional binary system in terms of area and power dissipation [1]. In this work, we want to extend the findings of [1] to a generic datapath for digital signal processing and show the advantages deriving from the use of the RNS in terms of flexibility and power dissipation.

Recently, reconfigurable hardware, such as FPGAs, has gained a large portion of the market because it allows fast prototyping and tuning-up of the products which reduce design time and costs. However, usually reconfiguration of FPGAs cannot be done at run time (on-the-fly).

Reconfigurable computers (RCC) are systems that combine a reconfigurable hardware processing unit with a programmable controller. The basic blocks are arithmetic units (such as multipliers and adders) which can be configured to implement a given algorithm or a sequence of computations. Reconfigurable computers are well suited for high-throughput and data-parallel applications [2]. RCCs offer less flexibility than FPGAs, but can be configured on-the-fly by a command string. The growing interest for reconfigurable computers is also confirmed by the appearance on the market of the first commercial systems [3].

In this paper, we present the design of a RNS configurable datapath oriented to DSP applications. Our datapath should be reconfigurable, or programmable, in terms of bit-width (dynamic range), type of operations (multiplication or addition), and sequence of operations. As a first approach, we selected an architecture of the datapath suitable for convolution and pattern matching.

2  Background

A Residue Number System is defined by a set of relatively prime integers {m₁, m₂, ¼, m_P }. The dynamic range of the system is given by the product of all the moduli m_i: M = m₁ ·m₂ ·¼·m_P .
Any integer X Î { 0, 1, 2, ¼M-1} has a unique RNS representation given by:

X RNS ®   ( áX ñm1, áX ñm2, ¼, áX ñmP )

where áX ñ_mi denotes the operation X mod m_i. Operations on single moduli are done in parallel

Z = X op Y   RNS ®      ì ï ï ï í ï ï ï î Zm1 = áXm1 op Ym1 ñm1 Zm2 = áXm2 op Ym2 ñm2 ¼       ¼       ¼ ZmP = áXmP op YmP ñmP

(1)

Therefore, the use of the RNS allows the decomposition of a given dynamic range in slices of smaller range on which the computation can be implemented in parallel [4]. The conversion RNS to binary is accomplished by the Chinese Remainder Theorem (CRT) [5].

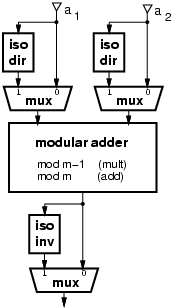
Modular multiplication can be simplified by using the isomorphism technique. According to [6], if m is prime there exists a primitive radix r such that its powers modulo m cover the set [1, m-1]. By using isomorphism, the product of the two residues is transformed into the sum of their indices which are obtained by an isomorphic transformation:

áa1 ·a2 ñm = áárw1 ñm ·árw2 ñm ñm = áráw1 + w2 ñm-1 ñm

(see [7] for implementation detail).

3  Datapath Architecture

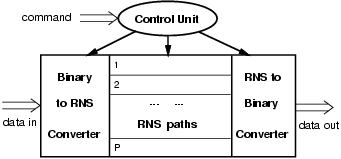
The RNS reconfigurable processor is depicted in Figure 1. The figure shows a control unit which is used to configure the datapath, according to a command string, to adapt it to different applications. The processor includes the conversions binary/RNS and RNS/binary.

There are three main advantages in using the RNS for a configurable datapath.

1. Once a dynamic range M₁ < M is chosen, and consequently, the number of bits required is smaller that the bit-width of the datapath (log₂ M₁ < log₂ M) we can turn-off in the RNS datapath the paths modulo m_i which are not needed to cover the dynamic M₁.

   For example, by choosing the following set of moduli: { 3, 5, 7, 11, 13, 17, 19} a 22-bit dynamic range can be covered. If our system requires a dynamic range of 16 bits we can use the set of moduli:
   { 3, 7, 11, 17, 19} turning off the paths through the moduli 5 and 13. As a consequence, for dynamic ranges smaller than the maximum range the power dissipation is reduced.

2. If the moduli m_i are chosen as prime numbers, we can apply the isomorphism technique, described above, and implement modular multiplication and addition with almost the same hardware, as sketched in Figure 2. Modular multiplication or addition can be programmed just by setting the multiplexers.

   As an alternative to Figure 2, because in RNS the dynamic range is broken down into smaller ranges of a few bits (3-6), we can implement any operation satisfying Expr. (1) with small look-up tables to be loaded during reconfiguration.

3. Because of the small bit-width of moduli m_i, local routing of wires to connect processing elements in a RNS path gives smaller wire-lengths than the routing in a full dynamic range datapath.

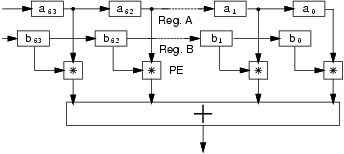
We designed our datapath to have a maximum dynamic range of 32 bits, 64 processing elements PEs (either multipliers or adders), and a tree of adders to add 64 operands. As a first implementation, for each of the RNS paths (see Figure 3), we connected the inputs of the PEs to two élog₂ m_iù-bit shift registers (Reg. A and B) and the output to the tree of adders. This scheme is suitable for mono and bidimensional convolution and pattern matching, as later explained. The RNS paths not used to cover a given dynamic range are deactivated by disabling the clock of registers A and B in the path.

A command string, a sort of micro-instruction, is given to the controller (Figure 1) to perform the following tasks:

• To set the dynamic range by selecting the required moduli paths in the controller and the datapath. This is done by disabling the clock signal in the paths not used.
• To set the operations to be performed in the PEs. This is done by setting a bit (add=0, mult=1) in the PEs of Figure 2
• To load the shift-registers.
• To stop/start the data acquisition/output for specific operations.

For the set of applications we selected, register A holds values which are constant for the whole processing. For this reason, we can use one binary to RNS converter to load both register A (at start-up) and register B (runtime). The RNS to binary converter is programmable in terms of dynamic range as well: when some moduli are not used in the datapath, the corresponding parts in the converter are disabled by switching off the clock in the registers at the interface between the RNS paths and the converter.

4  Applications and Datapath Configuration

4.1  FIR filters

The first application we implement on the reconfigurable RNS datapath is a a programmable 64-tap FIR filter

y(n) = 63 å k = 0  ak x(n-k)

realized in direct form. The dynamic range is adjusted to have an error free filter. The main feature of the filter is the reconfigurability in terms of dynamic range. The filter dynamic range is adapted to the processing specifications.

For this application, the coefficients a_k are loaded in register A and the samples x(n-k) are fed into register B one per clock cycle. The PEs are all set in multiply mode.

4.2  Bidimensional Convolution

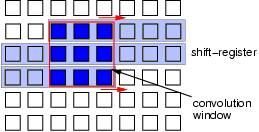
Bidimensional convolution is used to process an image in the time domain. Averaging, smoothing and sharpening of a digital image are done by the convolution of the matrix of pixels representing the image B(n×n) with a specific mask W(m×m). For example, if m = 3 the value of the new pixel is computed as:

B¢[x,y] = 1 å i = -1  1 å j = -1  B[x+i,y+j] ·W[i,j]

Shift register A is used to store the coefficients of the mask W. Using an approach similar to that in [8], we can extract windows of pixels from a single data stream, as in the case of the FIR filter. Pixels are fed line by line, from top to bottom, until two complete lines and three pixels of a third line are stored in the shift register B. At this point, see Figure 4, the first 3×3 convolution can be performed, and, from this moment on, each new pixel inserted in the shift register moves the convolution window one position. Because we can store up to 64 pixels in B, when the image is larger than 30 pixels (most cases), we have to cut the image in vertical bands 30 pixel-wide introducing an overhead, necessary to load B, when we reach the bottom line of the image and we have to reposition the convolution window at the beginning of the new band.

4.3  Pattern Matching

We consider the problem of detecting from a stream of data a sequence of symbols, where each symbol is represented by a word of n bits. If, as an example, we consider a stream of ASCII characters, we want to detect the 8-character sequence ÄB*A***D", in which the wildcard (*) indicates that any character can be in that position. A simple approach to perform the task, using the reconfigurable RNS datapath, consists in the following steps:

1. Load the complement of the residual representation of the sought pattern in register A. Load a zero when there is a wildcard.
2. Set the PEs to perform the following operations: multiplication in correspondence of wildcard/zero, addition otherwise.
3. Feed the character stream into shift-register B. If the output is zero the pattern is matched. otherwise is not.

Table 1 show an example of pattern matching using the two moduli { 11, 17}.

5  Implementation and results

The implementation of the reconfigurable RNS datapath has been realized with the AMS 0.35 mm library of standard cells. To cover the 32-bit dynamic range in RNS we chose the following set of moduli:

{ 13, 17, 19, 23, 29, 31, 64 }.

With these moduli, we have a granularity of four bits in scaling the dynamic range.

In order to compare the performance of the reconfigurable RNS processor in terms of throughput, area and power dissipation, we implemented a programmable 64-tap FIR filter realized in the traditional two's complement system (TCS) with 32-bit dynamic range. Table 2 reports the characteristics of the TCS filter and the reconfigurable RNS datapath. The table shows that the RNS processor is about 25% faster than the traditional FIR filter and consume less power (at the same frequency).

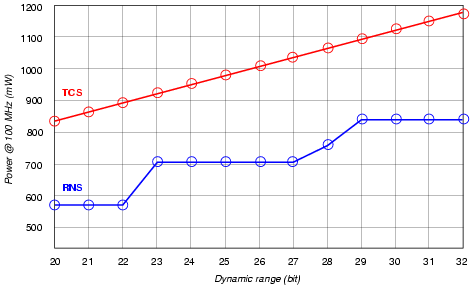
By reducing the dynamic range, we obtain for the power dissipation, computed at 100 MHz, the results shown in Figure 5. For the TCS filter the range is reduced simply by feeding data with shorter wordlength, while for the RNS datapaths, we also disabled, by turning off the clock, the paths through the moduli not necessary to cover that dynamic range. The figure shows that the TCS filter working at 20 bit dynamic range consumes almost the same energy of the RNS working at full dynamics. From the RNS set of points (staircase shape), we can see that the power reductions are due to the different configurations of active moduli, and, once a moduli set is selected, the power dissipation is constant. For the TCS, the set of points is on a straight line because by reducing the input wordlength, the most-significant portion of the datapath get filled with sign-extension bits¹, which significantly reduce switching activity.

6  Conclusions and future work

We presented the implementation of a RNS configurable datapath suitable for digital FIR filtering, bidimensional convolution and pattern matching. The datapath is configurable in terms of dynamic range and type of operations. We compared its performance and power dissipation with a FIR filter realized in the traditional two's complement system, and found that the RNS datapath can be clocked at a higher frequency and consumes on the average a 30% less power.

We plan to introduce an interconnection network between PEs in the datapath to improve its flexibility and be able to run more applications on it.

References

[1]

A. Nannarelli, M. Re, and GC. Cardarilli, ``Tradeoffs between Residue Number System and Traditional FIR Filters,'' Proc. of IEEE International Symposium on Circuits and Systems, vol. II, pp. 305-308, May 2001.

[2]

H. Singh, M.-H. Lee, G. Lu, F.J. Kurdahi, N. Bagherzadeh, and E.M. Chaves Filho, ``MorphoSys: an integrated reconfigurable system for data-parallel and computation-intensive applications,'' IEEE Transactions on Computers, pp. 465-481, May 2000.

[3]

Chameleon Systems, http://www.chameleonsystems.com/.

[4]

M.A. Sodestrand, W.K. Jenkins, G. A. Jullien, and F. J. Taylor, Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, New York: IEEE Press, 1986.

[5]

M. Re, A. Nannarelli, GC. Cardarilli, and R. Lojacono, ``FPGA Implementation of RNS to Binary Signed Conversion Architecture,'' Proc. of IEEE International Symposium on Circuits and Systems, vol. IV, pp. 350-353, May 2001.

[6]

I.M. Vinogradov, An Introduction to the Theory of Numbers, New York: Pergamon Press, 1955.

[7]

A. D'Amora, A. Nannarelli, M. Re, and GC. Cardarilli, ``Reducing Power Dissipation in Complex Digital Filters by using the Quadratic Residue Number System,'' Proc. of 34th Asilomar Conference on Signals, Systems, and Computers, pp. 879-883, Nov. 2000.

[8]

B. Bosi, G. Bois, and Y. Savaria, ``Reconfigurable Pipelined 2-D Convolvers for Fast Digital Signal Processing,'' IEEE Transactions on VLSI Systems, pp. 299-308, Sept. 1999.

Footnotes:

¹Radix-4 Booth recoding in multipliers transforms a sequence of 1s (negative numbers) in a sequence of 0s.