Copyright 2000 IEEE. Published in the Proceedings of 34th Asilomar Conference on Signals, Systems, and Computers, pages 879-883, Asilomar Hotel and Conference Grounds, Pacific Grove, CA, USA. Oct. 29 - Nov. 1, 2000.

Reducing Power Dissipation in Complex Digital Filters by using the
Quadratic Residue Number System ¹

Angelo D'Amora, Alberto Nannarelli, Marco Re and Gian Carlo Cardarilli
Department of Electrical Engineering
University of Rome "Tor Vergata" - Italy

http://dspvlsi.uniroma2.it/

Abstract

1  Introduction

The new generation of telecommunication equipment often require the use of high order FIR filters for the implementation of the new modulation schemes. Moreover, low power consumption for new portable multimedia terminals is needed. In this context, computational intensive signal processing blocks can be effectively implemented by using Residue Number System (RNS) arithmetic.

The use of the RNS allows the decomposition of a given dynamic range in slices of smaller range on which the computation can be efficiently implemented in parallel [1], [2], [3]. The QRNS (Quadratic RNS) is particularly convenient when dealing with complex numbers [4] [5]. In QRNS the imaginary term of a complex number is transformed into an integer, therefore a complex multiplication which requires four integers multiplications and two sums in the conventional two's complement system, is implemented with two integer multiplications in QRNS.

The drawback presented by the RNS (and QRNS) is the overhead due to both input and output conversions binary-RNS-binary. This problem can be solved by using efficient conversion techniques [6] [7], or by converting directly the analog signal in the residue representation [8].

Recently, a number of works on low power and RNS have been presented. In [9] and [10] the power dissipation is reduced by taking advantage of the speed-up due to the parallelism of the RNS structure. The supply voltage is reduced, resulting in a quadratic reduction of power, until the speed-up = 1 [9], or until the desired value of delay [10]. In [11] some encoding optimization techniques for small moduli are presented.

In our work, we compare the performance, area and power of a complex FIR filter realized with the traditional binary arithmetic, with a QRNS based one.

Both filters have been designed according to the specifications of an actual filter used in a telecommunication satellite and are clocked at the same rate of 166 MHz. Although the QRNS filter has a longer latency, it can sustain the same throughput of the traditional one, while its area and power dissipation are about 57% of the total area and 34% of the total power of the traditional filter.

2  Background

A Residue Number System is defined by a set of relatively prime integers

{m1, m2, ¼, mP }  .

The dynamic range of the system is given by the product of all the moduli m_i:

M = m1 ·m2 ·¼·mP .

Any integer X Î { 0, 1, 2, ¼m-1} has a unique RNS representation given by:

X RNS ®   ( áX ñm1, áX ñm2, ¼, áX ñmP )

where áX ñ_mi denotes the operation X mod m_i. Operations on single moduli are done in parallel

Z = X op Y   RNS ®      ì ï ï ï í ï ï ï î Zm1 = áXm1 op Ym1 ñm1 Zm2 = áXm2 op Ym2 ñm2 ¼           ¼           ¼ ZmP = áXmP op YmP ñmP

The conversion of the RNS representation of Z can be accomplished by the Chinese Remainder Theorem (CRT):

Z = P å i = 0    mi   ·á mi   -1   ñmi ·Zmi  M       with mi   = M mi

and [`(m<sub>i</sub>)]<sup>-1</sup> obtained by á[`(m_i)] ·[`(m_i)]^-1 ñ_mi = 1.

In the complex case, we can transform the imaginary term into an integer if the equation q²+1 = 0 has two distinct roots q₁ and q₂ in the ring of integers modulo m_i (Z_mi). A complex number x_R + j x_I = (x_R, x_I) Î Z_mi, with q root of q²+1 = 0 in Z_mi has a unique Quadratic Residue Number System representation given by

(xR, xI) QRNS ®   (Xi, ^ Xi   )     i = 0, 1, ¼, P Xi = áxR + g ·xI ñmi ^ Xi   = áxR - g ·xI ñmi

The inverse QRNS transformation is given by

xR = á2-1 (Xi + ^ Xi   ) ñmi xI = á2-1 ·q-1 (Xi - ^ Xi   ) ñmi

where 2^-1 and q^-1 are the multiplicative inverses of 2 and q, respectively, modulo m_i:

á2 ·2-1 ñmi = 1    and     áq ·q-1 ñmi = 1  .

Moreover, it can be proved that for all the prime integers which satisfy

p = 4k +1                 k Î N

the equation q² +1 = 0 has two distinct roots q₁ and q₂.

As a consequence, the product of two complex numbers x_R + j x_I and y_R + j y_I is in QRNS

(xR + j xI)(yR + j yI) QRNS ®   ( áXi Yi ñmi, á ^ Xi   ^ Yi   ñmi )

and it is realized by using two integers multiplications instead of four. Table 1 shows an example of QRNS multiplication in the ring modulo 13.

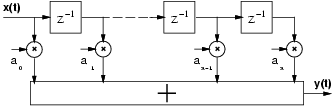
A complex N taps FIR filter (Figure 1) is expressed by

y(n) = N å k = 0  ak x(n-k)

where x, y, a_k denotes complex quantities. From the QRNS theory described above, it is easy to derive for the complex filter the structure shown in Figure 2, in which both portions of the filter are realized with P RNS filters working in parallel.

3  Traditional FIR Filter

The starting point of our design is a programmable 64-tap FIR filter realized in direct form (Figure 1) with complex input and coefficients size of 10 bits for the real part and 10 bits for the imaginary part. These data are derived from the specification of an actual digital filter, used aboard a satellite for direct TV broadcasting. We designed a prototype filter in traditional two's complement system in order to compare its performance, area and power dissipation with a QRNS filter.

The filter can be decomposed in a real and imaginary part. A single tap is realized as sketched in Figure 3. The real and imaginary products are realized with two Booth multipliers [12] and the resulting partial products are accumulated in a Wallace's tree structure which produces a carry-save (CS) representation of the product in each side of the filter. The CS representation of the products, is then accumulated in two 128-addend Wallace's tree realized with 4:2 compressors [13], not depicted in Figure 3. To have an error-free filter we must keep a number of bits sufficient to hold the carry-save representation of the sum, and we need a 20 + log₂ 64 wide tree. The carry-save representation is finally converted into two's complement representation by a carry-propagate adder (realized with a carry-look-ahead scheme) in the last stage of the filter (both real and imaginary sides).

The filter has been implemented in the AMS 0.35 mm standard cells library, and it was synthesized from VHDL description using Synopsys and a constraint of 6 ns as a critical path, for this reason it resulted in a pipelined filter of 6 stages.

4  QRNS FIR Filter

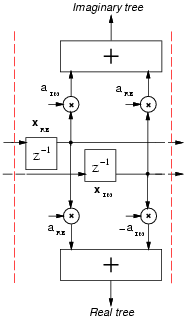From Figure 2 we can see that the QRNS filter can be realized by two RNS filters in parallel. Each RNS filter is then decomposed into P filters working in parallel, where P is the number of moduli used in the RNS representation. In addition, the RNS filter requires both binary to QRNS and QRNS to binary converters. In order to have a dynamic range of 20 bits, as in the case of the traditional implementation, we chose the following set of moduli:

mi = { 5, 13, 17, 29, 41 }

such that

log2 ( 5 ·13 ·17 ·29 ·41 ) = 20.3 .

4.1  Implementation of modular multiplication

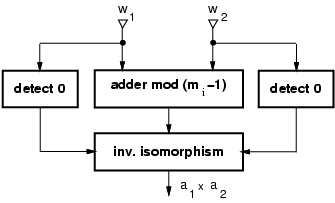
In each tap, a modular multiplier is needed to compute the term áa_k x(n-k)ñ_mi. Because of the complexity of modular multiplication, we used the isomorphism technique [14] to implement the product of residues. By using isomorphism, the product of the two residues is transformed into the sum of their indices which are obtained by an isomorphic transformation. According to [14], if m is prime there exists a primitive radix r such that its powers modulo m cover the set [1, m-1]:

ni = árwi ñm        with ni Î [ 1, m-1] wi Î [ 0, m-2].

Both transformations n ® w and w ® n can be implemented with m-1 entries tables. Therefore, the product of a₁ and a₂ modulo m can be obtained as:

áa1 ·a2 ñm = árw ñm

where

w = áw1 + w2 ñm-1         with a1 = árw1 ñm a2 = árw2 ñm

In order to implement the modular multiplication the following operations are performed:

i) Two isomorphic transformations to obtain w₁ and w₂;
ii) One modulo m-1 addition áw₁ + w₂ ñ_m-1;
iii) One inverse isomorphic transformations to obtain the product.

For example, for the modular multiplication

á3 ·4 ñ5 = 2

we have (r = 2):

i) 3 = á23 ñ5 ® w1 = 3 4 = á22 ñ5 ® w2 = 2 ii) á2 + 3 ñ4 = 1 iii) á21 ñ5 = 2

The input x, although delayed, is the multiplicand of all the multiplications (see Figure 1). For this reason only one isomorphic transformation, incorporated in the binary to QRNS conversion, is necessary for all the taps. On the other hand, because the coefficients of the filter (multiplicators) are constant terms loaded once at start-up, it is convenient to load directly the isomorphic representation modulo m_i-1. As a result, in each tap, we reduce the modular multiplication to a modular addition followed by an access to table (inverse isomorphism) as depicted in Figure 4. The table is implemented as synthesized logic and special attention has to be paid when one of the two operands is zero. In this case, there exists no isomorphic correspondence and the modular adder has to be bypassed.

4.2  Implementation of modular addition

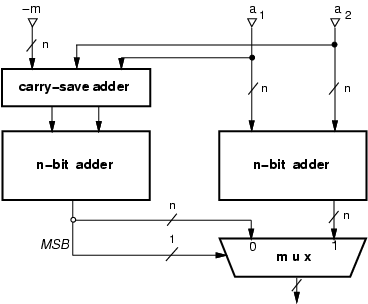
The modular addition áa₁ + a₂ ñ_m, consists of two binary additions. If the result of a₁ + a₂ exceeds the modulo (it is larger than m-1), we have to subtract the modulo m. In order to speed-up the operation we can execute in parallel the two operations:

(a1 + a2)     and     (a1 + a2 - m).

If the sign of the three-term addition is negative it means than the sum (a₁ + a₂) < m and the modular sum is a₁ + a₂, otherwise the modular addition is the result of the three-term addition. The above algorithm can be implemented with two élog₂ mù-bit adders as shown in Figure 5.

At the output of the tree, it is necessary to reduce the sum S of all the taps to áS ñ_mi . This is done with the modulo-reduction technique described in [6].

4.3  Implementation of input/output conversions

As already mentioned, the input conversion block includes the isomorphic transformation. If x is zero, there is no exponent w such that ár^w ñ_mi = 0. As a consequence, zero is encoded with a special pattern that is then detected in the block which computes the product using the isomorphism (Figure 4).

The output conversion is implemented by using the Chinese Remainder Theorem (CRT), as described in [6].

5  Results and Comparisons

Both the traditional and the QRNS filters were implemented in the AMS 0.35 mm standard cells library. Delay, area and power dissipation have been determined with Synopsys tools.

Table 2 summarizes the results. In the table, area is reported as number of NAND2 equivalent gates and power is computed at 166 MHz. However, both area and power dissipation do not take into account the contribution of interconnections.

Table 2 shows that the QRNS filter has a higher latency, due to the conversions, but it can be clocked at the same rate of the traditional filter, and consequently, it can sustain the same throughput. However, the QRNS filter is almost half the area on the traditional complex filter, and consumes one third of the energy.

6  Conclusions

We have implemented a QRNS 64-taps FIR filter and compared its delay, area and power dissipation with those of a corresponding complex FIR filter realized with the traditional two's complement system. The results obtained show that the QRNS filter can sustain the same clock rate, although it has a slightly longer latency. However, in terms of area and power the QRNS version is more convenient. A better improvement is expected for filters with a larger number of taps.

Acknowledgements

References

[1]

N.S. Szabo and R.I. Tanaka. Residue Arithmetic and its Applications in Computer Technology. New York: McGraw-Hill, 1967.

[2]

M.A. Sodestrand, W.K. Jenkins, G. A. Jullien, and F. J. Taylor. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing. New York: IEEE Press, 1986.

[3]

M.A. Soderstrand and K.Al Marayati. Vlsi implementation of very high-order fir filters. IEEE International Symposium on Circuits and Systems (ISCAS'95), Vol. 2:1436-1439, 1995.

[4]

F. J. Taylor, G. Papadourakis, A. Skavantzos, and A. Stouraitis. A radix-4 FFT using complex RNS arithmetic. IEEE Transactions on Computers, Vol. C-34:573-576, June 1985.

[5]

M. Abdallah and A. Skavantzos. On the binary quadratic residue system with noncoprime moduli. IEEE Transactions on Signal Processing, Vol. 45:2085-2091, Aug. 1997.

[6]

G. Cardarilli, M. Re, and R. Lojacono. A residue to binary conversion algorithm for signed numbers. European Conference on Circuit Theory and Design (ECCTD'97), Vol. 3:1456-1459, 1997.

[7]

G. Cardarilli, M. Re, R. Lojacono, and G. Ferri. A new efficient architecture for binary to rns conversion. Proc. of European Conference on Circuit Theory and Design (ECCTD'99), Vol. 2:1151-1154, 1999.

[8]

A.P. Preethy and D. Radhakrishnan. A vlsi architecture for analog-to-residue conversion. Third International Conference on Advanced A/D and D/A Conversion Techniques and Their Applications, pages 83-85, 1999.

[9]

M. Bhardwaj and A. Balaram. Low power signal processing architectures using residue arithmetic. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ASSP'98), Vol. 5:3017-3020, 1998.

[10]

W.L. Freking and K.K. Parhi. Low-power digital filters using residue arithmetic. Thirty-First Asilomar Conference on Signals, Systems and Computers, Vol. 1:739-743, 1998.

[11]

M.N. Mahesh and M. Mehndale. Low power realization of residue number system based fir filters. Thirteenth International Conference on VLSI Design, pages 30-33, 2000.

[12]

Israel Koren. Computer Arithmetic Algorithms. Prentice-Hall, Inc. , 1993.

[13]

M.D. Ercegovac and T. Lang. Division and Square Root: Digit-Recurrence Algorithms and Implementations. Kluwer Academic Publisher, 1994.

[14]

I.M. Vinogradov. An Introduction to the Theory of Numbers. New York: Pergamon Press, 1955.

Footnotes:

¹34th Asilomar Conference on Signals, Systems, and Computers, Asilomar Hotel and Conference Grounds, Pacific Grove, CA, USA. Oct. 29 - Nov. 1, 2000.