
Figure 4.1: Design flow and tools.
The techniques presented in Chapter 3 are applied to double-precision division/ square root units, which implement the algorithms described in Chapter 2. First, we give an overview of the design flow and the tools and the libraries of standard cells used. Then, we present the implementations of division for radix-4, 8, 16, and 512, and the implementation of a radix-4 combined division and square root unit. For each scheme, we provide the energy consumption for the basic, or standard, and low-power implementations and an estimate of a possible implementation with dual-voltage and by optimizing some blocks with Synopsys Power Compiler. In the presentation of the units, we highlight the differences from the implementation of the radix-4 divider, set as the reference. However, for sake of clarity and completeness, some repetitions of concepts and figures occur. Detail of the implementation of blocks, which are common to many units, is given in Appendix A.
The most convenient way of describing the units under investigation is to use a hardware description language, in this case VHDL which allows the description and simulation of the system at different level of abstraction and the use of hierarchy. The design flow we used is depicted in Figure 4.1.

Figure 4.1: Design flow and tools.
The behavioral and RT-level are handled by Synopsys Tools [37]. Synopsys provides a number of tools to generate, maintain and simulate a VHDL description of the circuit. The interface between the RT-level and the physical level is handled by COMPASS Tools [38]. COMPASS provides ASICSynthesizer a logic synthesizer that maps the VHDL behavioral description of a block into gates. However, ASICSynthesizer performs synthesis by optimizing only delay and area. COMPASS also provides an automatic floor-planner for the layout generation and a simulator at gate-level (Qsim), for the simulation of pre-layout and layout-extracted netlists. The design can be divided into the following steps (or levels):
In addition, synthesis using Synopsys Power Compiler was performed. As explained later in Section 4.2, the results of the synthesis of large blocks are not completely satisfactory. For this reason, we limit the synthesis with Power Compiler to the selection function, which is a small and irregular block. First the design with the shortest delay is synthesized, and then, incrementally, a new compilation is done to optimize the design for power dissipation trying not to increase the delay.
As explained in Section 1.5, in order to compute the energy dissipated in a circuit, information on the capacitance (layout) and on the circuit activity (simulation or statistics) are required. This computation is done by PET: Power Evaluation Tool (Appendix B Section B.1), which computes the energy dissipated in a circuit from the layout-extracted netlist, the standard cell library characteristics, and the results of a logic-level simulation run on a given set of test vectors.
The average energy/power dissipation can be determined by applying random-generated input patterns (test vectors) and monitoring the energy dissipated using a simulator. This approach belongs to the Monte Carlo methods [39]. Monte Carlo simulations give an accurate estimate of the expected value with a limited number of trials (test vectors) [40].
The estimation error, derived from [41], for a normal distribution of the energy values can be written as:
| (17) |
| (18) |
The same approach to estimate the total average power dissipation on a set of benchmark circuits is presented in [42]. For those benchmark circuits, simulations on about 10 random vectors are sufficient to have an estimation error smaller than 5%. Moreover, according to [42], the validity of expression (4.2) can be extended to any distribution for small values of s.
At the end of the chapter, in Section 4.7 at page pageref we summarize the error obtained for the estimation of the energy dissipated in the units presented in this work.
The units were realized using the Passport 0.6 mm, 3.3 V, three-metal layers, standard cell library [43] and the layout was obtained by automatic floor-planning. The percent reductions in the energy dissipation indicated below might vary for different technologies and layout styles. The critical path, unless otherwise specified, is computed post-layout and takes into account the RC-effect of interconnections.
The Passport library was designed to operate with VDD = 3.3 V and COMPASS tools cannot implement more than one supply voltage. In order to evaluate the application of dual voltage, we performed SPICE simulations on a 4-bit carry-ripple adder to determine the dependency of the delay with respect to VDD (Figure 4.2). The delay is normalized to the one for VDD = 3.3 V. The plot shows that for VDD = 2.0 V the delay is doubled, and that for voltages below 1.7 V the delay increases in excess.
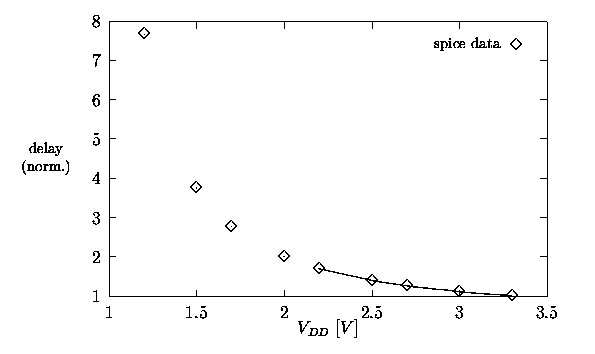
Figure 4.2: Delay (normalized) with different V
The energy consumption for dual voltage was estimated on a block basis, by using the following expression:
| (19) |
The first assumption was verified by counting the actual number of transitions detected by the logic simulator at the input of the blocks in question, while SPICE simulations on a 4-bit slice of the recurrence showed that the second assumption leads to an over-estimation because the value provided by expression (4.3) is about 10% larger than the actual energy dissipation for values of V2 from 3.3 V to 2.0 V.
The library of standard cells used in Synopsys Power Compiler is different from the one used in COMPASS. This is due to the fact that the Passport library, used in COMPASS, is not characterized, both timing and power, for Synopsys. The library used in Synopsys is the ST CB45000 Standard Cell, 0.35 mm 5 layer metal HCMOS6 process, with power supply voltage of 2.7 V [44].
Databook comparisons and testing on small circuits showed that the CB45000 library at 2.7 V is about 33% faster than the Passport library at 3.3 V.
For each of the units below, we present four implementations. The first implementation is the one obtained with the only constraint of minimum delay. This implementation is also indicated as standard and abbreviated std in the tables. The second implementation is the low-power implementation obtained by applying the techniques described in Chapter 3. This implementation is indicated as l-p in the tables. With our library and tools it is not possible to realize layouts which use dual voltage (Section 3.6). For this reason we can provide just estimates of dual voltage implementations, which are abbreviated d-v in the tables. Estimates of the energy dissipation after to optimization with Synopsys Power Compiler are indicated as syn in the tables.
4.6 Radix-4 Combined Division and Square Root
4.7 Summary of Estimation Error