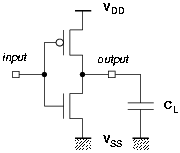
Figure 1.1: CMOS inverter loaded with C
The main purpose of this chapter is to provide the necessary background for the concepts and the methods presented in this work. First, we introduce the metrics used to evaluate the energy and power dissipation and illustrate the main sources of energy consumption in VLSI circuits based on static CMOS technology. Then, we discuss different approaches aiming to reduce the energy dissipation, and a list of simulation and optimization tools, at different levels of abstraction, is presented. In the last part of the chapter, the IEEE format for floating-point and its utilization for division and square root are briefly described.
In this work a common measure of the energy dissipation is required in order to evaluate and compare different approaches in low-power design. Because the algorithms are in general different and the latency of the operations varies from case to case, it is convenient to have a measure of the energy dissipated to complete an operation. This energy-per-operation is given by
|
|
|
|
| (1) |
Over the past decade, CMOS technology has played a dominant role in the market of digital integrated circuits, and it is expected to continue in the near future. For this reason, this work is focused on CMOS systems. Two components characterize the amount of energy dissipated in a CMOS circuit [9]:
The total energy dissipation for a CMOS gate can be written as
| (2) |
The quantity Eload is the energy dissipated for charging and discharging the capacitive load CL when ni output transitions occur. If in a gate (like the one in Figure 1.1) one transition from the logic level "low" (VSS = 0 V) to "high" (VDD) occurred1 at time t, we can write
| (3) |
| (4) |

Figure 1.1: CMOS inverter loaded with C
The energy due to the short-circuit current is Esc. In a CMOS inverter (Figure 1.1), during a transition both the n and the p-transistors are on for a short period of time. This results in a short current pulse from the power supply voltage (VDD) to ground (VSS). With no loading the short-circuit current is quite relevant, while by increasing the output loading the current drawn for charging or discharging the capacitance, becomes dominant. Esc depends on VDD, the transition time, the gate design, the load CL and ni ([11] pages 92-97).
The energy due to leakage currents Eleakage is small and usually neglected, unless the system spends a large amount of time in stand-by or sleep status.
In the analysis of more complex gates, especially in standard cells libraries, the energy is usually split into two contributions:
Therefore, the expression of the average energy dissipated in a cell is
| (5) |
For a circuit composed of several cells, the energy dissipation can be computed as the sum of the energy dissipated in each cell. That is,
| (6) |
Several techniques have been developed to reduce the energy dissipation of CMOS systems. By expression (1.2) and expression (1.4), the minimization can be carried out by reducing the supply voltage, the capacitance, the number of transitions (e.g. the activity in the circuit), and by optimizing the timing of the signals and the design of the gate to reduce the energy due to short-circuit currents.
A large impact on energy is made by the supply voltage. By reducing VDD the energy dissipation decreases quadratically, but the delay increases and the performance is degraded. A possible solution is that of using different supply voltages in different parts of the circuit [12]. The parts not in the critical path are supplied by lower voltages, while the critical one by the higher voltage [13]. Another technique is to compensate the loss of performance by replicating the hardware (parallelism) to keep the throughput [14].
Capacitance can be reduced at different levels. At transistor, or layout, level by keeping the size of the device small and by optimizing the wire interconnection capacitance during the floor-planning and the routing. At gate level, by using gates specially designed for low-power and by merging a set of gates into a more complex cell eliminating the interconnection capacitance [15]. It is important to note that by reducing the capacitance, not only the energy dissipation, but also the performance will be improved.
The number of transitions can be reduced at transistor level, by equalizing the delay of the different paths to avoid the generation of glitches [16], and at register-transfer (RT) level, by disabling both combinational and sequential blocks not used at a particular time [17]. Combinational logic can be disabled by forcing a constant logic value at its inputs, while in sequential circuits this can be obtained by disabling the clock [18]. This last technique, known as clock gating, can be also implemented at gate-level by gating the clocks to individual flip-flops [19]. Retiming is the circuit transformation that consists in re-positioning the registers in a sequential circuit without modifying its external behavior [20]. By retiming it is possible to stop the propagation of glitches reducing the activity in the system. A combined optimization of number of transitions and capacitance is obtained by swapping a pin whose activity is high with a pin with lower capacitance [15].
Further reduction are achieved by changing the data encoding and the algorithm [21], [13].
The energy dissipation due to short-circuit currents can be reduced by careful design at gate level and by buffering in order to avoid long transition (rise/fall) times [11].
Finally, energy dissipation can be reduced by changing the fabrication process to support very low-voltages, copper interconnects, and insulators with low dielectric constants [1].
In this work, we reduce the energy by applying minimization technique at RT-level and gate-level. Optimization of short-circuit energy dissipation and transistor level techniques are not covered.
Recently there has been a renewed interest in asynchronous circuits due to the potential better power efficiency over the traditional synchronous (clocked) systems ([11] pages 461-492).
Clocked circuits waste energy by clocking all parts of the chip whether or not they are doing useful work. Clock trees are also responsible for a significant portion of the energy dissipated in the chip. In asynchronous circuits the number of transitions is reduced, but the self-timing requires the use of additional logic for control signals. There is a tradeoff between number of transitions and capacitance (extra logic).
In this work, the research on low-power division and square root is limited to synchronous circuits.
Examples of a self-timed divider and of a self-timed shared division and square root unit are presented in [22] and [23], respectively. The area of the latter unit, as stated in [23], is about 1.7 larger than the corresponding synchronous implementation. However, no information on power or energy dissipation is provided in the articles in question, and a comparison with the corresponding synchronous units is undoable because of unknown parameters such as circuit activity and switching capacitance.
Computer-aided design (CAD) tools are used to speed-up the design process and improve the productivity. As mentioned above, techniques for low-power integrated circuits (IC) design can be applied at every level of abstraction and some CAD tools that take into account power constraints, in addition to the traditional delay and area constraints, start to be available [11].
In the design of a system two fundamental aspects are analysis and optimization. CAD tools analyze a system to extract information on performance, area and power dissipation. This information is then used to evaluate if the designed system met the constraints and/or to optimize the design. Estimators for average energy dissipation can be either based on simulation or on probabilistic models of the energy dissipated in a circuit, or on statistical estimation techniques [24].
Methods based on simulation give good accuracy and are straightforward to implement. Simulations at transistor level monitor the power supply current waveform, at higher level the number of transitions is counted and energy is estimated by expression (1.6), or equivalent. However, simulation methods are pattern-dependent and in an early phase of the design, patterns generated by several functional blocks might be still unknown. Furthermore, the simulator and the energy estimator can either be tightly-coupled or loosely-coupled [25]. In tightly-coupled systems the estimation is done at run time, while in loosely-coupled systems the simulator outputs the transition statistics on a file for the energy estimator. The main advantage of the latter is the flexibility: different simulators can be used in different design stages.
The estimation using probabilities alleviates the pattern-dependency problem. Instead of simulating the circuit for a large number of patterns and then averaging the result, one can assume a distribution of the probability of the inputs and use that information to estimate how often internal nodes switch. Signal probabilities are propagated into the circuit assuming different timing, probability propagation and energy models that, depending on the specific tools, take into account temporal and spatial correlation of the signals, short-circuit energy and so on. To some extent, the process is still pattern-dependent because the user has to supply the probabilities of the inputs. However, this information might be more readily available than specific input patterns. The drawback of these estimators is that they use simplified models, so that they do not provide the same accuracy as circuit simulations. Better accuracy can be obtained at expenses of more complicated models and longer execution times. There is a tradeoff between accuracy and speed.
Statistical methods do not require specialized models. They use traditional simulation models and simulate the circuit for a limited number of randomly generated input vectors while monitoring the energy. Those vectors are generated from user-specified probabilistic information about the circuit inputs. Using statistical estimation techniques, one can determine when to stop the simulation once a specified estimation error is obtained. Details of these methods are given in Section .
In general, it is not clear which is the best approach, but statistical methods offer a good mix of accuracy, speed and ease of implementation [24].
CAD tools can be differentiated by the level of abstraction at which they operate. We describe below, tools to perform analysis and synthesis for low-power.
Tools for estimation at transistor level achieve the best accuracy, but require the longest run time. At this level, energy evaluation is done by simulations and SPICE is the reference among the simulators. However, other commercial tools claim an accuracy within 5% of SPICE and execution times up to x1000 faster [25]. Transistor level estimators are typically used to characterize cells and modules for use at the higher abstraction levels.
Optimization at this level is done by tools which resize the transistors according to given power/delay/area constraints [25].
Energy estimation at gate level is less accurate than energy estimation at the transistor level, but it is faster and can be done in an earlier stage of the design with good accuracy (10-15%). Energy values can typically be reported by signal, gate or blocks of gates.
Optimization is done by using several techniques (refer to Section 1.3) to reduce the energy under given timing constraints. One popular commercial tool with power optimization capability is Synopsys Power Compiler [26].
At this level estimation is mainly done with probabilistic models by analyzing VHDL or Verilog descriptions of the system. The accuracy is in the range 20-25%, but large circuits can be analyzed in a short time at an early stage of the design [1]. A commercial tool available for estimation at this level is Sente WattWatcher/Architect [27].
Optimization at this level is currently an interactive process, consisting in the evaluation of various design alternatives and the subsequent choice of the design that best fits the project constraints [1].
The IEEE floating-point standard 754 defines formats for binary representation of floating-point numbers [2]. The two basic formats are the single-precision 32-bit format and the double-precision 64-bit format. We now, briefly describe the double-precision format which is the one used in the rest of this work.
The 64 bits of the double-precision format are divided into three fields: 1-bit field representing the sign S, a 11-bit field representing the biased exponent E, and a 52-bit field f which represents the fractional part of the significand (1.f). Thus, the floating-point number F is represented by the following expression
|
When performing the division of two floating-point numbers X and D, such as:
|
|
An alternative to post-normalization is pre-shifting. Pre-shifting is done before performing the division by shifting one of the operands to obtain x ³ d and consequently, q is already normalized in [1, 2).
In square root,
|
|
| |||||||||||||||||||
In the rest of this work, we describe only the operations (division and square root) to be performed on the significands and we treat rounding assuming that the operands are pre-shifted.
1 One transition from VDD to VSS produces identical results.