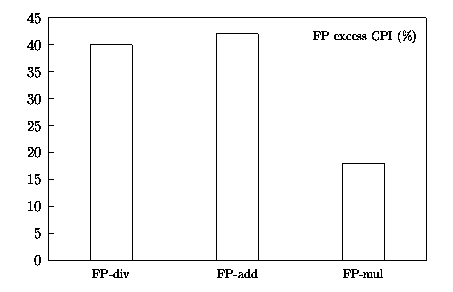
Figure 0.1: FP-unit stall time distribution.
In recent years the demand for low-power electronic systems has increased due to both the massive advent of portable devices, which require small and light batteries, and the increased densities on chip and the consequent necessity of reducing the energy dissipated.
In digital systems the number of transistors on a chip doubles every two years and the smaller device size allows the use of faster clocks. As a consequence, the charging and the discharging of many devices due to more frequent transitions of the signals causes an increase of energy dissipation. This increase in energy consumption results in many side effects that can increase the cost of the system or even compromise its functionality.
It is reported that current microprocessors, such as the Pentium or the Alpha, dissipate about 30 W [1]. A system that dissipates more than 2 W cannot be placed in a plastic package and the use of ceramic packaging, heat sinks, and coolant fans raises significantly the cost of the product. Moreover, a chip that dissipates 30 W at 3.3 V requires wires on the circuit board that can deliver a current of about 10 A.
More serious problems can arise in case of large current densities, since electromigration, caused by large currents flowing in narrow wires, might produce gaps or bridges in the power-rails of the chip with a consequent permanent damage of the system.
The possibility to put entire systems on a chip and the miniaturization of I/O devices (displays, sensors, etc...), brought on the market a variety of portable products such as cellular phones, laptop computers, personal digital assistants (PDA), GPS receivers, and medical devices. The critical resource of these systems is the battery lifetime, which can be lengthened by reducing the energy dissipation. This reduction also enables the use of smaller, and lighter, batteries. A cellular phone that requires a battery recharge every hour or a laptop computer powered by a car battery are not very practical. For this reason it is essential that portable systems be designed for low-power.
This work investigates the implementation of low-power double-precision floating point division and square root units compliant with the IEEE standard [2]. These units are common in general-purpose processors, but the results obtained can be extended also to units with a different number of bits implemented in DSP cores or other application-specific processors.
Although division and square root are not very frequent ignoring their implementations can result in system performance degradation [3]. We briefly summarize some facts stated in [3]. Table 0.1 shows the average frequency of floating-point (FP) operations in the SPECfp92 benchmark suite. By assuming a machine model of a scalar processor, where the FP-adder and FP-multiplier have both a latency of 3 cycles and the FP-divider has a latency of 20 cycles, a distribution of the excess CPI (cycles per instruction) due to stalls in the FP-unit is shown in Figure 0.1. The stall time is the period during which the processor was ready to execute the next instruction, but the dependency upon an unfinished FP-operation prevented it from continuing. This excess CPI reduces the overall performance by increasing the total CPI. Figure 0.1 shows that, although division is less frequent than addition and multiplication, its longer latency accounts for 40% of the performance degradation. For this reason, many general-purpose microprocessors implement division in hardware and try to make it fast enough not to compromise the overall performance.
| Percent of all FP instructions | |
| division | 3 % |
| square root | 0.3 % |
| multiplication | 37 % |
| addition | 38 % |
| other | 21 % |

Figure 0.1: FP-unit stall time distribution.
As for the energy dissipation, no data on the comparison of division with other FP operations are available in literature. In [4] (pages 194-198), a quite coarse evaluation is done using only the number of transitions to estimate the energy dissipation of a radix-2 and a radix-4 divider, without an actual implementation. Because this evaluation did not take into account the switching capacitance and only the recurrence part of the low radices 2 and 4 is evaluated, the results obtained do not illustrate very well the design issues of low-power dividers. The implementations of a FP-adder and FP-multiplier, realized by the same group of people with the same technology, are described in [5] and [6], respectively. Table 0.2 summarizes the data of the two implementations.
| FP-adder | FP-multiplier | |
| technology | CMOS 0.5 mm, 3.3 V | CMOS 0.5 mm, 3.3 V |
| fMAX | 164 MHz | 286 MHz |
| Area | 2.5 ×3.5 mm2 | 4.2 ×5.1 mm2 |
| n. pipeline stages | 5 | 5 |
| Energy per | 3.24 mW/MHz | 5.10 mW/MHz |
| operation | Eadd = 16 nJ | Emul = 25 nJ |
In order to evaluate what percentage of the energy consumption is dissipated in the divider, we implemented with our library the 54 × 54-bit multiplier described in [7] and determined the energy consumed per multiplication which resulted to be Emul = 15 nJ . By assuming the same ratio [(Emul)/(Eadd)] as in Table 0.2, we estimated the energy consumed in a FP addition as Eadd = 10 nJ . Finally, we computed the energy dissipation for the radix-4 divider of Section 4.2, which resulted to be Ediv = 40 nJ . Combining these values with the instruction mix of the program spice (see Table 0.3 [8]), we obtained the breakdown for the energy dissipated in the FP-unit shown in Figure 0.2.
| Instruction | Percent | Unit |
|
division | 8 % | FP-div |
|
multiplication | 26 % | FP-mul |
|
addition | 14 % | |
| subtraction | 22 % | |
| comparison | 7 % | |
| move | 2 % | |
|
| 45 % | FP-add |
|
other | 20 % | - |
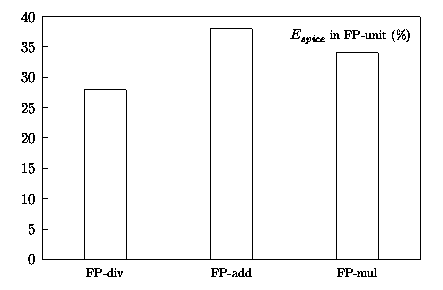
Figure 0.2: Breakdown of energy in FP-unit.
Figure 0.2 shows that although division is less frequent than addition and multiplication, because of its longer latency, it dissipates about 30% of the total energy consumed in the floating-point unit when running the program spice. Consequently, it is important that division unit be designed for low-power. For these reasons, we explore the possibilities of reducing the energy dissipated in division and square root units. Our main objective is to reduce the energy consumption without increasing the execution time. However, we also consider tradeoffs between delay and energy in some cases. Furthermore, we study the relation between energy dissipation and the radix of division and square root implementation.
The research is carried out by implementing, with a static CMOS standard cell library, a set of division and square root units, and by applying several techniques aiming to reduce the energy dissipation. Since the energy dissipated in CMOS cells is proportional to the number of transitions, to the output load, and to the square of the operating voltage [9], we reduce the number of transitions, the capacitance and estimate the impact of using a lower voltage. For the energy reduction, we separate the units into two portions, the recurrence and the on-the-fly conversion and rounding [10]. In the first portion, we retime the recurrence to reduce the glitches and to constrain the critical path to the most-significant slice. This allows the replacing in the non-critical slice of the radix-2 carry-save adder cell by a radix-r version to reduce the number of flip-flops. Moreover, in the non-critical slice we use low-drive and low-voltage cells. Finally, we equalize the signal paths to reduce the glitches. For the on-the-fly conversion and rounding, we modify the algorithm to reduce the number of flip-flops and their activity. For these low-activity flip-flops, we use individual gated clocks to reduce the energy of the flip-flops that do not change. In addition, we implement gated trees to reduce the energy in the distribution of signals. The energy dissipation is computed from the actual implementations in most cases, and estimated in others.
Results show that the energy dissipated to complete one operation is almost constant for several radices, and that in most cases it is possible to reduce the energy dissipation between 40 and 60 percent without increasing the latency.
This work is organized as follows. Chapter 1 introduces background concepts related to energy dissipation and the standards used in the number representation. Chapter 2 presents the algorithms used to perform division and square root. Chapter 3 describes the techniques and methodologies used to reduce the energy dissipation. Chapter 4 presents the actual implementations of the units and the application of the techniques of Chapter 3. Chapter 5 summarizes the results obtained and discusses some of the tradeoffs among different implementation. Finally, Chapter 6 draws the conclusions.