Modelling confinement loss in practical small-core holey optical fibres
Vittoria Finazzi and Tanya M. Monro
Optoelectronics Research Centre, University of Southampton,
SO17 1BJ, UK. Email: vf@orc.soton.ac.uk
ABSTRACT:
Microstructured optical fibres (MOFs) are all-silica fibres that guide light
by means of an arrangement of air-holes that run down the entire fibre
length. In the kind of MOFs here considered, also named holey fibres (HFs),
guidance arises from average-index effects: the holes form the cladding
region around the solid core. The modes of such fibres are leaky because
the core refractive index is the same as the index beyond the (finite)
cladding region. HFs with a core diameter of the scale of an optical
wavelength and large holes have been fabricated, resulting in the smallest
effective area ever measured in a fibre at 1550nm [1]. Such small
effective areas make these fibres attractive for nonlinear applications. The
cladding of a HF is usually comprised of hexagonally-packed rings of
holes, and when the hole-to-hole spacing (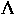 )
is of the order of the wavelength, several rings of holes
are required to reduce the confinement loss to a practical value. Fibre
fabrication feasibility on the other hand constrains the number of rings that
can be used. Therefore in order to optimise the design of this class of fibres,
it is necessary to study the loss characteristics for small-core HFs.
)
is of the order of the wavelength, several rings of holes
are required to reduce the confinement loss to a practical value. Fibre
fabrication feasibility on the other hand constrains the number of rings that
can be used. Therefore in order to optimise the design of this class of fibres,
it is necessary to study the loss characteristics for small-core HFs.
To perform this study we applied the multipole method recently developed
in Ref. [2]. This method considers MOFs with a finite cladding region of
circular holes and performs full-vector modal calculations. This method
yields the complex propagation constant, and thus the confinement losses
can be calculated via the imaginary part. It uses polar coordinate systems
centred in every hole, therefore no-false birefringence is introduced and
the symmetry properties of the structure are preserved. The location of the
circular holes is arbitrary, although they cannot overlap.
Fig. 1 shows a sample calculation of the modal characteristics of the
2-degenerate fundamental mode for a 3-ring structure with
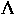 =1.2
=1.2 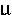 m
and holes of diameter d=1.08
m
and holes of diameter d=1.08 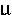 m.
The calculated propagation constant is neff=1.29584423675 + i 9.825
x10-9, corresponding to a loss of 0.35 dB/m and an effective
area of 1.75
m.
The calculated propagation constant is neff=1.29584423675 + i 9.825
x10-9, corresponding to a loss of 0.35 dB/m and an effective
area of 1.75 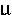 m2 at 1550nm, that is of
the same order of the one reported in Ref. [1] for a real HF.
The confinement loss for small-core
HFs as a function of the number and dimension of the holes and of the
modal effective area will be presented and discussed.
m2 at 1550nm, that is of
the same order of the one reported in Ref. [1] for a real HF.
The confinement loss for small-core
HFs as a function of the number and dimension of the holes and of the
modal effective area will be presented and discussed.
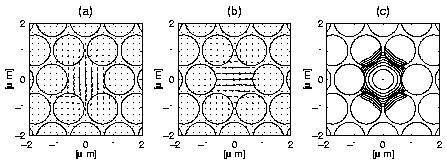
Degenerate fundamental mode:
(a) transverse electric and (b) magnetic fields; (c) Normalized poynting
vector (contours spaced by 2 dB). See text for MOF structure details.
REFERENCES:
-
P. Petropoulos, T.M. Monro, W. Belardi, K. Furusawa, J.H. Lee, and
D.J. Richardson,
``2R-regenerative all-optical switch based on a highly nonlinear
holey fiber,''
Opt. Lett. 26, 1233-1235 (2001).
-
T.P. White, R.C. McPhedran, C.M. de Sterke, and L.C. Botten,
``Multipole method for efficient microstructured optical fiber calculations,''
in Proc. CLEO, Baltimore, 2001, OSA Technical Digest, paper JTuC6.
