We consider the MI of optical beams in media with a purely quadratic (or x(2)) nonlinearity, analysing in detail the instability gain spectra when linear and nonlinear quasi-phase-matching (QPM) gratings are present. Because such spectra can now be measured in the laboratory2, studying their profiles has direct experimental relevance.
We find that, due to the periodicity, novel low- and high-frequency bands appear in the gain spectrum, each with fundamentally different physical origins. The high-frequency gain bands are a general feature of gain spectra for QPM gratings, related to the inherent MI in the non-phase-matched, gratingless x(2) material. In contrast, the low-frequency bands depend critically on the modulation depths and periods, and can totally disappear for particular gratings. Induced by the phase-matching periodicities, they are accurately predicted by a simple average theory.
Our results show that when the low-v gain bands are suppressed, dark solitons can propagate stably over experimentally relevant distances, due to the residual high-v gain being typically small. This increases the potential utility of dark solitons in applications, allowing their particular advantages to be exploited1.
This research is supported by the Danish Technical Research Council through Talent Grant No. 26-00-0355.REFERENCES:
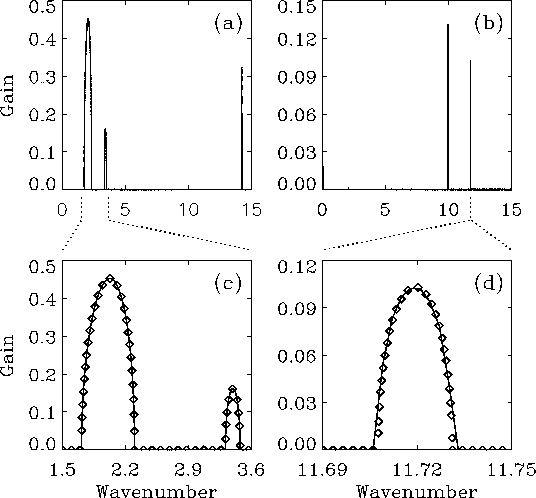 Gain spectra for (a) LiNbO3 and (b) GaAs/AlAs gratings.
Diamonds give average theory results in (c) and equivalent homogeneous
results in (d).
Gain spectra for (a) LiNbO3 and (b) GaAs/AlAs gratings.
Diamonds give average theory results in (c) and equivalent homogeneous
results in (d).